Gemeinsamkeiten
Um die Grundlagen für diese Aktivität zu haben, empfiehlt es sich die Repetition Konstanten und die
Repetition Funktionen durchgearbeitet zu haben.
Sie werden durch dieses Curriculum schrittweise zur Abstraktion geführt, welche die folgenden fünf Schritte beinhaltet, wobei die letzten vier Schritte als Refactoring in einer gemeinsamen Aktivität zusammengefasst werden:
- Muster bzw. Gemeinsamkeiten finden
- Unterschiede suchen
- Parametrisieren
- Extrahieren
- Vereinen
- Benennnen
In dieser Aktivität wir der Fokus auf die Gemeinsamkeiten bzw. dadurch auch auf die Unterschiede in Grafiken und Codefragementen gelegt. Damit sollen Sie künftig einerseits strukturierter an die Zerlegung (decompose) von Grafiken herangehen sowie Codefragmente kritischer betrachten, um mögliche Codeduplikationen zu erkennen und diese durch Abstraktion möglichst soweit wie möglich zu vermeiden.
Gemeinsamkeiten und Unterschiede Vol. 1
Auf den ersten Blick wirken die beiden untenstehenden Bildern identisch, jedoch verstecken sich in diesen insgesamt 8 Unterschiede.

Lösungsbild

Gemeinsamkeiten und Unterschiede Vol 2.

Lösung
Viele Wege führen nach Rom
Es gibt viele Ansätze, wie man dieses konkrete Problem lösen kann, doch welcher ist nun der beste bzw. der effizienteste?
Wenn es sich, wie oben um ein Suchbild handelt, ergibt es vielleicht Sinn, sich zuerst auf die Unterschiede (wie z.B. die Accessoires) zu konzentrieren und diese systematisch abzusuchen.
Möchte man dieses Bild jedoch programmieren, so wäre es effizienter, sich zuerst auf die Gemeinsamkeiten der Hasen zu konzentrieren, sodass man festhalten kann, was alle sicher gemeinsam haben. Anschliessend kann man die Hasen noch individuell nach Unterschieden absuchen.
Muster finden
Schauen Sie sich die Figuren auf dem folgenden Bild genau an:

Hier einige Gemeinsamkeiten die man zwischen den Figuren feststellen kann:
- Es tragen alle Figuren Kleidung und haben eine Frisur.
- Sie haben alle die gleiche Schuhform.
- Sie haben alle die gleiche Hosenform (ohne Einbezug des Musters)
- Es haben alle den gleichen Gesichtsausdruck.
- Es haben alle dieselbe Körperhaltung.
- Die Frauen...
- ...tragen alle dieselbe Frisur.
- ...tragen alle ein T-Shirt mit V-Ausschnitt & ohne Kragen.
- Die Männer...
- ...tragen alle dieselbe Frisur, die sich aber von derjenigen der Frauen unterscheidet.
- ...tragen entweder ein T-Shirt mit V-Ausschnitt mit oder ohne Kragen.
Mustersuche Ying-Yang
Nun möchten wir dieses Konzept von der Mustersuche auf eine einzige Grafik transferieren, denn auch hier soll während des Zerlegungsvorgangs stets analysiert werden, ob innerhalb einer Grafik Symmetrien existieren oder ob es Teillösungen gibt, die wiederkehrend vorkommen.

Lösung
Beim Ying-Yang herrscht eine Symmetrie, welche gut ersichtlich wird, sobald man diese Grafik zerlegt. Im folgenden Bild wurden bereits ähnliche Teillösungen gruppiert, sodass man sehen kann welche Formen mehrmals innerhalb dieser Grafik vorkommen:
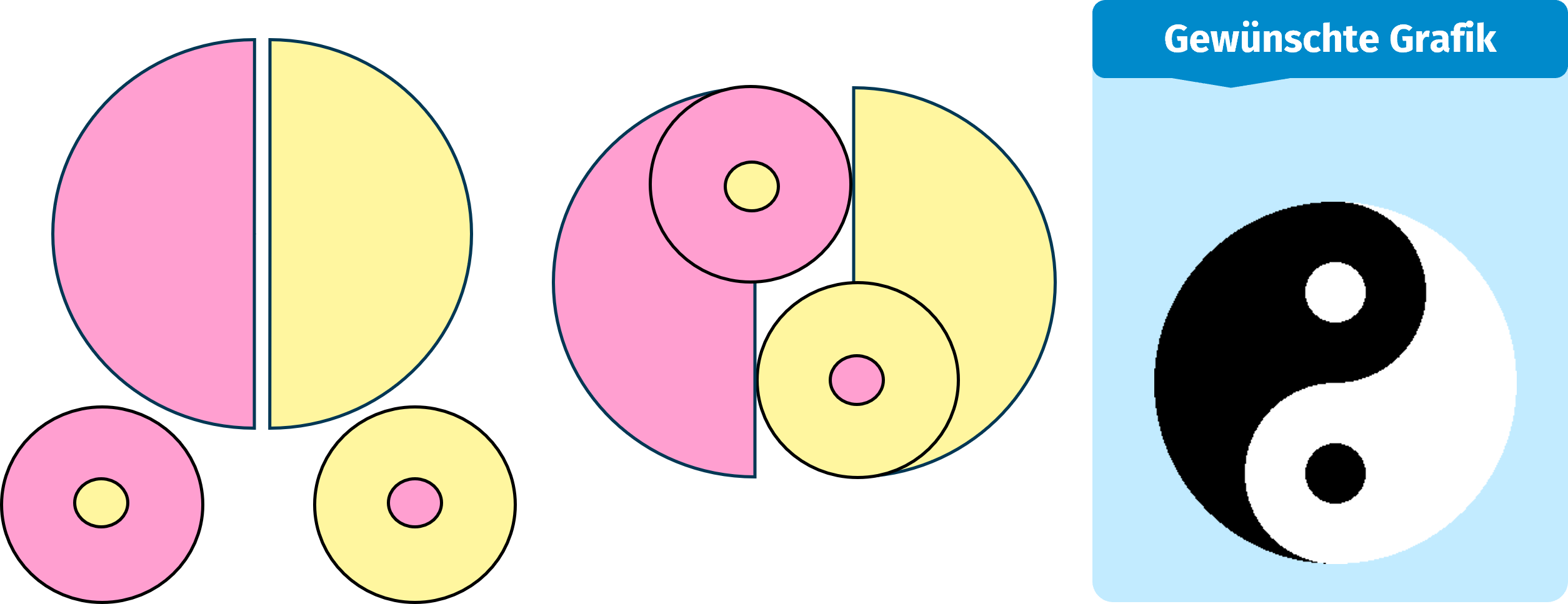
Codeanalyse Ying-Yang
Nun möchten wir von der Grafik zum Code hinübergehen und den folgenden Lösungsansatz etwas genauer betrachten:
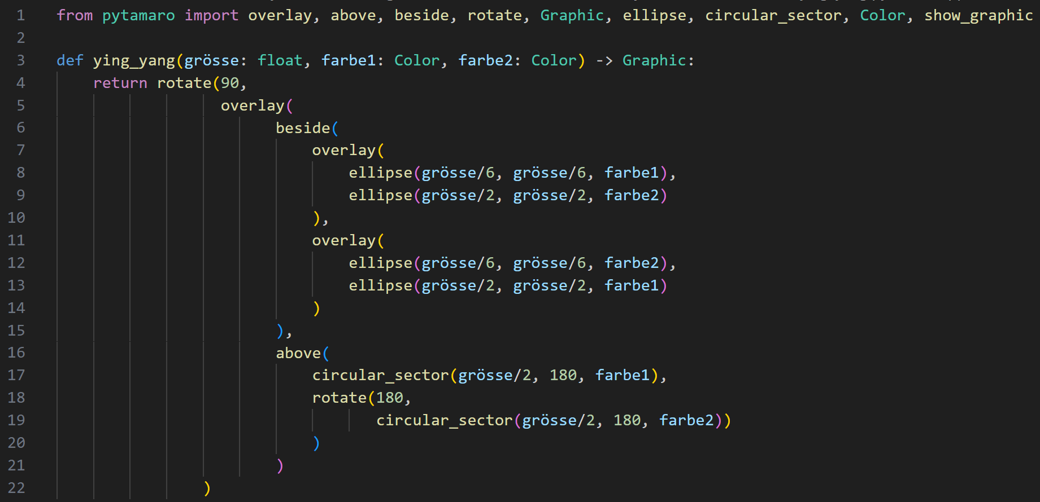
Codeduplikation Ying-Yang
Im folgenden Bild ist die Codeduplikation im Code vom Ying-Yang farblich gekennzeichnet:
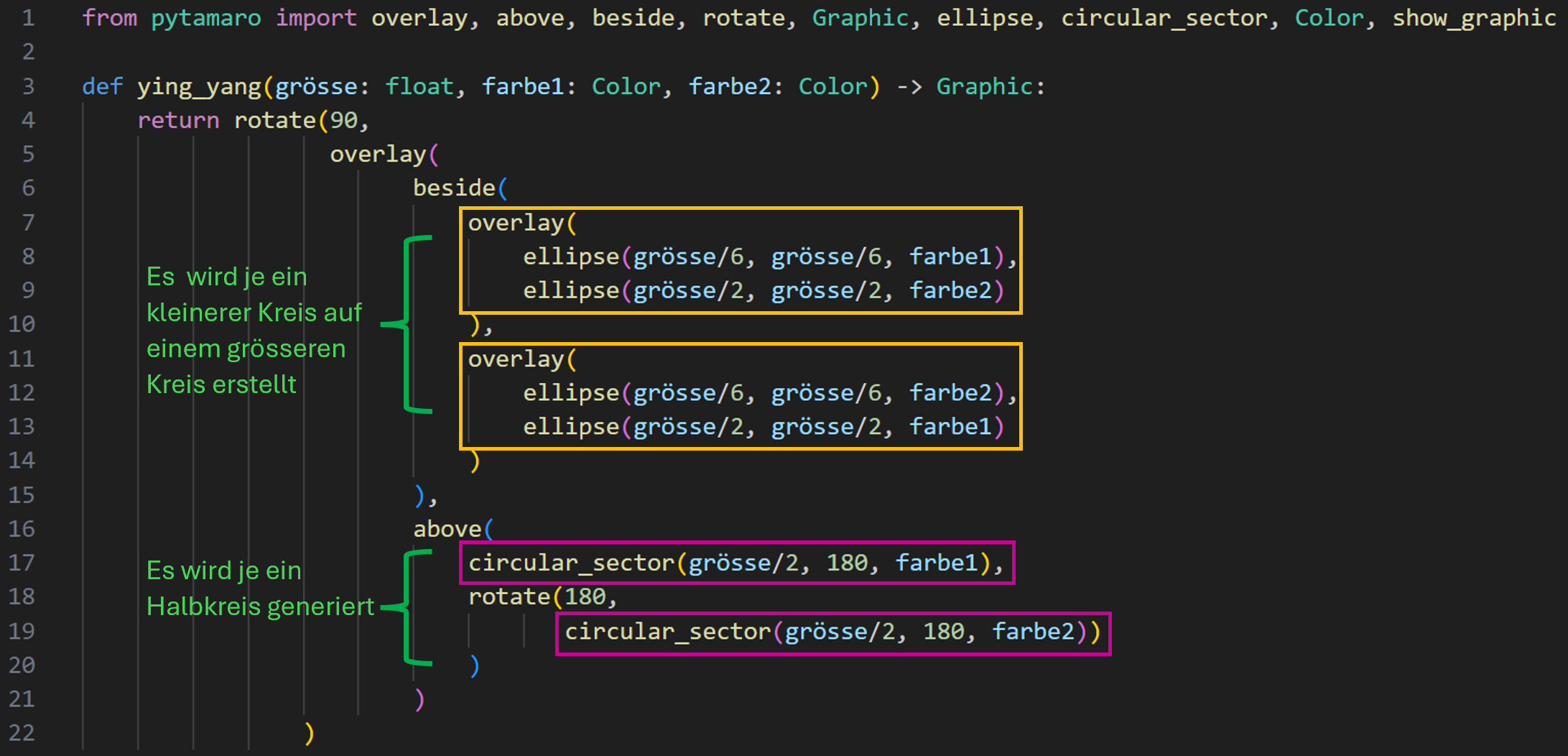
Die beiden in orange markierten Codefragmente erzeugen jeweils einen kleineren Kreis, welcher auf einem grösseren Kreis liegt. Somit wäre es doch sinnvoll, für diese beiden Codefragmente eine neue separate Funktion zu schreiben, bei welcher die Farbe flexibel gehalten werdenn kann und so die Codeduplikation minimiert wird.
Die in lila markierten Codefragmente erzeugen jeweils einen Halbkreis, der als Hintergrund der jeweiligen Hälfte dient.
Auf die weiterführende Verarbeitung dieser und der nachstehenden Grafiken wird in den nächsten Aktivität genauer eingegangen.
Mustersuche Gnom

Lösung
Einige Gmeinsamkeiten, die die Gnome aufweisen, sind:
- Alle tragen eine Mütze, einen Bart, Schuhe und ein Kleidungsstück.
- Alle besitzen eine Nase.
Eine mögliche Zerlegung eines einzelnen Gnoms könnte wie folgt aussehen:
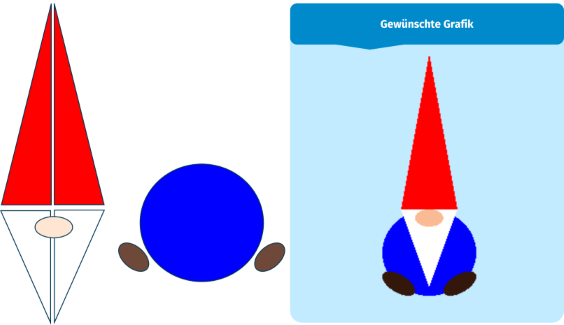
Wie Sie im obigen Bild sehen können, wurde sowohl der Hut als auch der Bart aus je zwei rechtwinkligen Dreiecken erstellt. So umgehen wir die Winkelberechnung, die Sie vermutlich noch nicht gelernt haben. Aber dass die Höhe in einem gleichschenkligen Dreieck die Grundseite in zwei gleiche Teilstücke teilt, sollten Sie wissen.
Die restlichen Elemente bestehen alle je aus einer Ellipse, nicht aus einem Kreissektor, dies ist insbesondere bei länglichen Gnomen gut ersichtlich.
Codeanalyse Gnomkopf
Nun wollen wir schauen, ob wir diese Muster auch nochmals im Code für den Gnomkopf sehen:
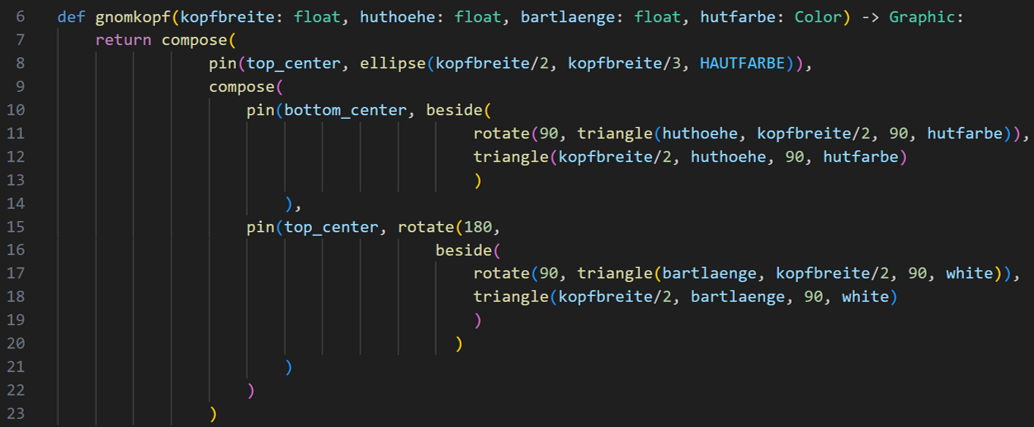
Codeduplikation Gnomkopf
Die Codeduplikation ist orange markiert:
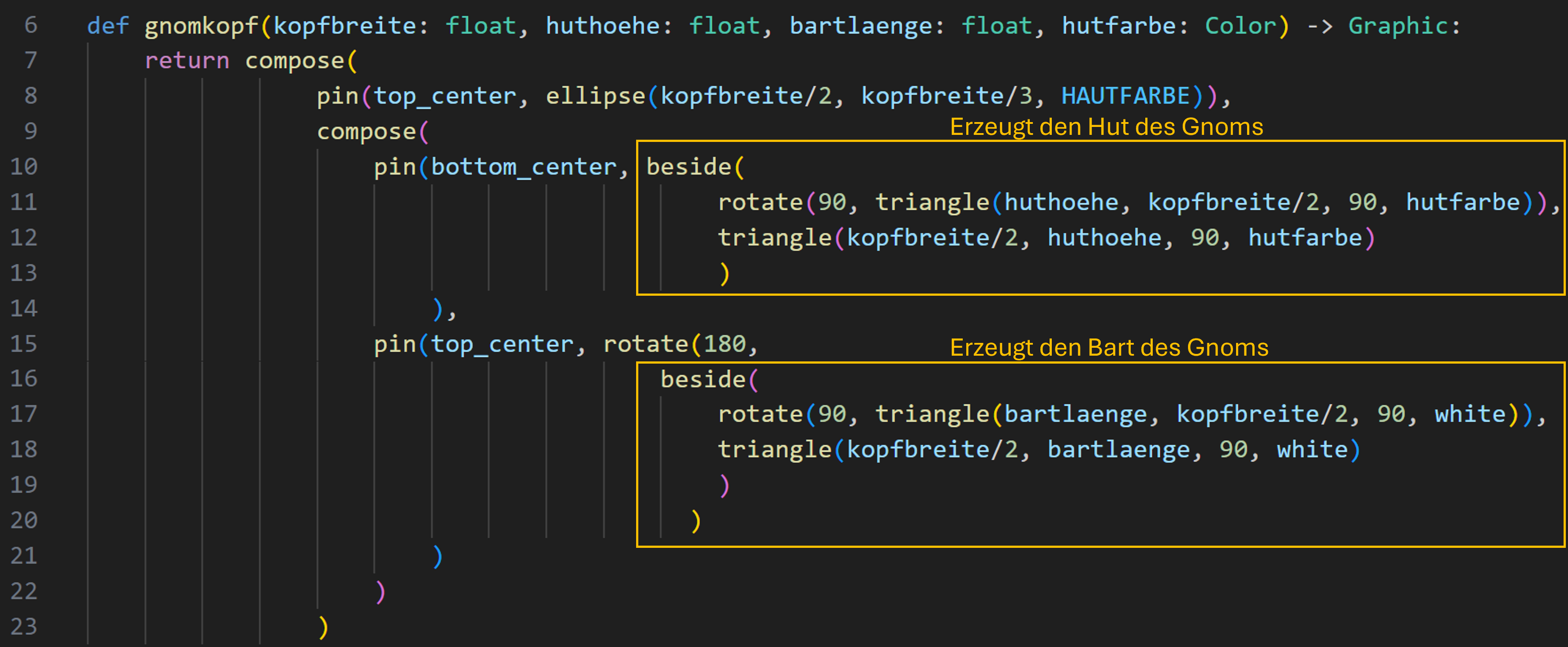
Das erste Codefragment ist für den Hut zuständig und das zweite für den Bart des Gnoms. Diese beiden Elemente wurden auch bei der grafischen Zerlegung als wiederholende Muster ausgewiesen.
Lösung
Auch hier würde es Sinn ergeben, die beiden Codefragmente in einer einzigen Funktion zusammenzufassen, was in einer nächsten Aktivität gemacht wird.
Codeanalyse kompletter Gnom
Hier sehen wir Code, der je einen ganzen Gnom in rot-blau und einen in gelb-grün erzeugt:
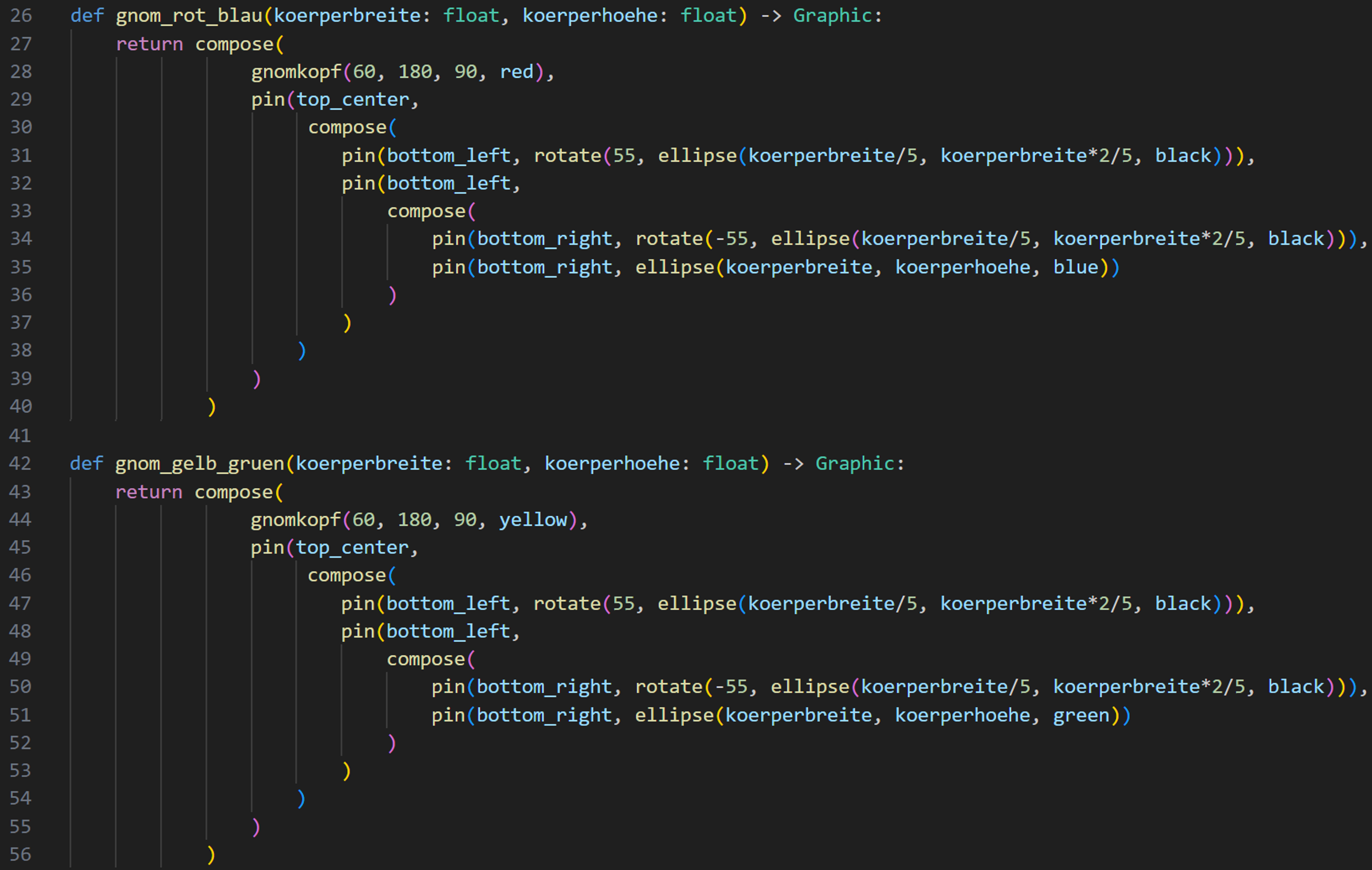
Codeduplikation Gnom
Wie im Bild ersichtlich, erwarten die beiden Funktionen bei ihrem Aufruf extakt die gleichen Parameter (in Magenta markiert) und auch der Funktionskörper ist im Aufbau identisch (in Orange):
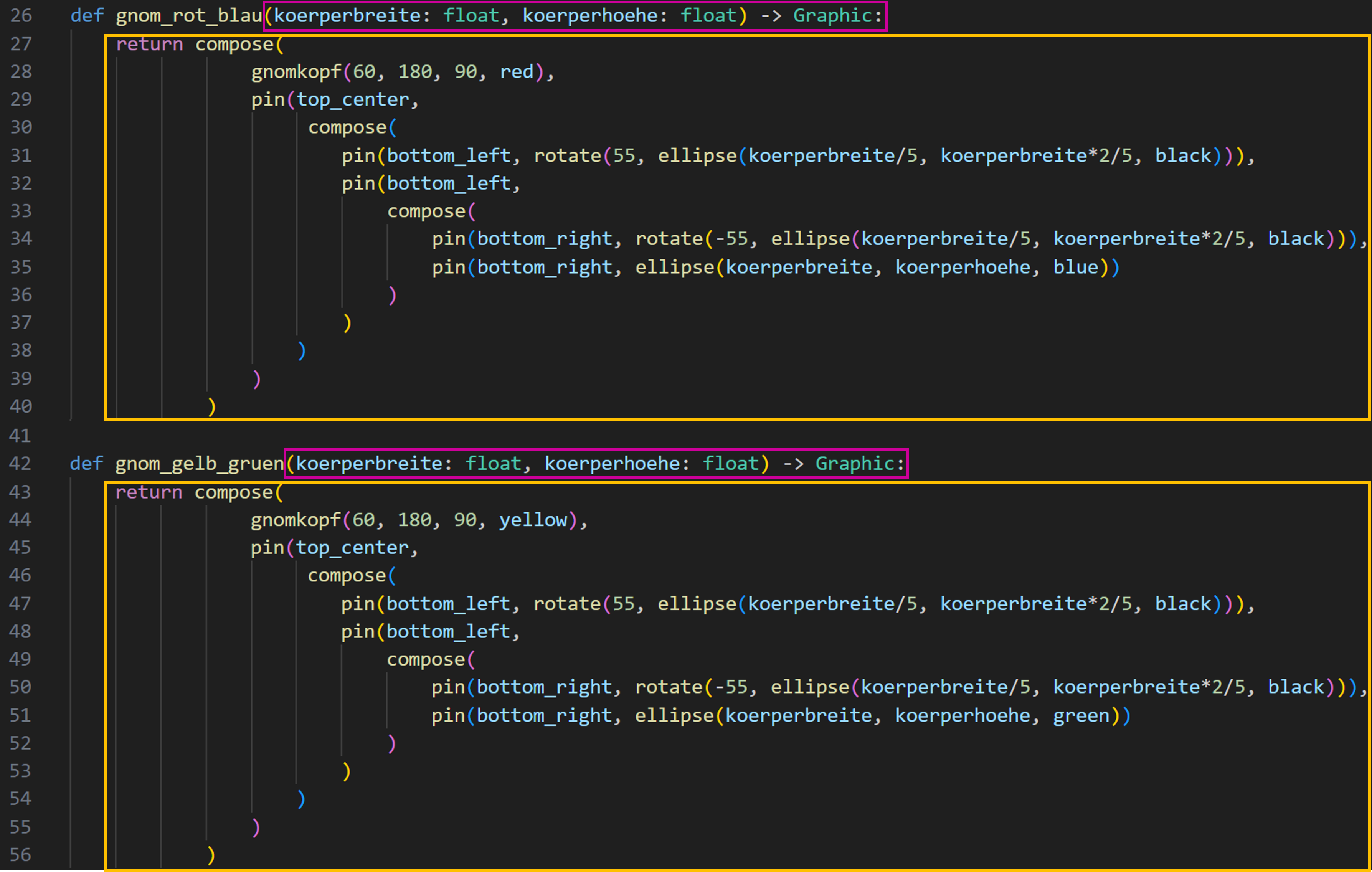
Würde man nun für jeden oben abgebildeten Gnom diese Vorgehen wählen, würde der Code enorm lang werden und zudem würden wir eine enorme Codeduplikation erzeugen. Somit würde es wohl Sinn ergeben, eine einzige Funktion gnomvariation() zu erstellen, um alle Gnome auf dem Bild und noch viele mehr erzeugen zu können.
In der folgenden Aktivität wir auf die Unterschiede in den eben hier analysierten Grafiken und Codefragmente eingegangen, was ebenfalls als Vorarbeit für die anschliessende Überarbeitung der entsprechenden Codes dient.
Was haben Sie in dieser Aktivität gelernt
Sie haben in dieser Aktivität...
- ...Gemeinsamkeiten (und Unterschiede) in Bildern gesucht.
- ...reflektiert, ob Sie bei Ihrer Analyse der Grafiken jeweils bei den Gemeinsamkeiten oder bei den Unterschieden ansetzen.
- ...Grafiken zerlegt und diese auf wiederkehrende Muster untersucht.
- ...den Code von Grafiken verglichen und nach gleichen Codefragmenten gesucht.
- ...gelernt, dass es ressourcensparender ist Grafiken aus eben diesen gefundenen Teillösungen, statt immer wieder aus den gleichen primitiven Bausteinen zusammenzusetzen.
- ...gelernt, dass für ein effizientes Programmieren die Mustersuche der erste Schritt sein muss.
This activity has been created by Schnider and is licensed under CC BY-SA 4.0.
Gemeinsamkeiten


PyTamaro is a project created by the Lugano Computing Education Research Lab at the Software Institute of USI
Privacy Policy • Platform Version a71e35c (Mon, 25 Aug 2025 18:25:55 GMT)
