At My Fingertips
Rapid Playground
Grafikkomposition mittels Fixierung
In dieser Aktivität wirst du schrittweise zwei Funktionen schreiben, die ein dreiblättriges bzw. ein vierblättriges Sauerkleeblatt generieren.
Die Teilblätter 1
Als Erstes musst du eine teilblatt Funktion implementieren, die ein Herz zurückgibt, da die Teilblätter eines Blattes als Herzen dargestellt werden können. Nutze dazu die halbkreis Funktion aus der Tulpe-Aufgabe der letzten Aktivität, die du in deiner Toolbox gespeichert hast.
Wenn du Schwierigkeiten hast, die Grafik zu zerlegen, schau sie dir an, wenn sie um 45 Grad im Uhrzeigersinn gedreht wird:
Sieht dein Teilblatt nicht wie ein Herz aus, sondern wie eine der beiden Varianten unten?
Lass uns das Problem mit den Papiergrafiken verdeutlichen!
Vorher kommentiere aber sämtliche Codezeilen in der Codezelle oben aus! Führe dann die Codezelle nochmals aus. Es darf keine Fehlermeldung mehr erscheinen.
Funktionen für die Grafikkomposition mittels Fixierung
++++++++++++++++Einführung der Thematik "Fixierung" mit den Papiergrafiken durch die Lehrperson++++++++++++++++
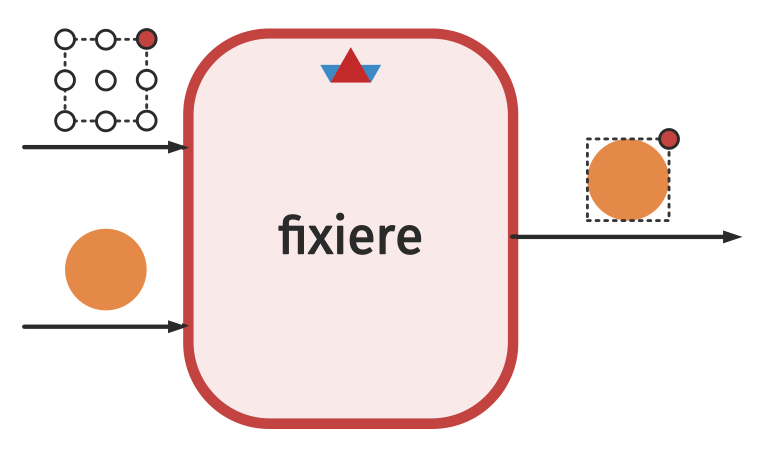
Führe die folgende Codezelle aus.
Die korrekte Antwort lautet: Die Fixierposition liegt in der Mitte des Kreises, aus dem der Kreissektor ausgeschnitten wurde.
Diesen Satz findest du in der Dokumentation der kreis_sektor Funktion.
Wenn du bei irgendeiner Grafik wissen willst, wo ihre Fixierposition liegt, kannst du das in Erfahrung bringen, indem du die Grafik der zeige_grafik Funktion übergibst und, durch ein Komma getrennt, den Wahrheitswert True als zweites Argument anfügst. In der Ausgabe markiert dann ein roter Rahmen den Begrenzungsrahmen der Grafik und ein gelbliches Kreuz gibt die Fixierposition an.
Gehe zurück zu der letzten Codezelle und ändere die Code-Stücke so ab, dass bei jeder Grafik der rote Rahmen und das gelbliche Kreuz mit angezeigt werden.
Die Teilblätter 2
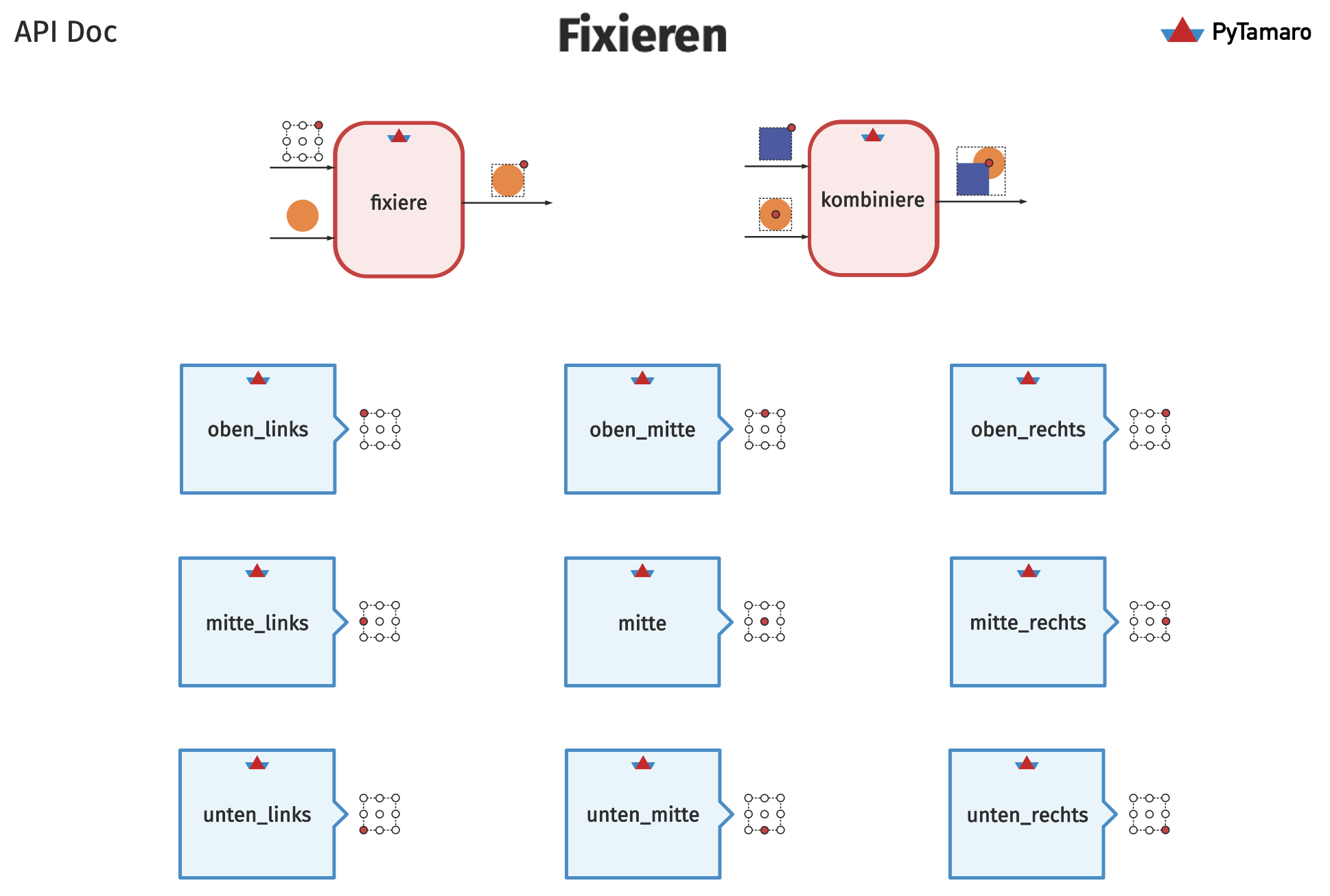
Schreibe nun die teilblatt Funktion mithilfe der neuen Funktionen fixiere und kombiniere, sowie den passenden Fixierpositionen, wie z.B. oben_links.
Speichere die teilblatt Funktion in deiner Toolbox ab. Du wirst sie in der nächsten Aktivität wieder nutzen können.
Der Blattstiel
Schreibe nun die blattstiel Funktion, die ein Rechteck der gewünschten Farbe zurückgibt. Das Rechteck soll 1/5 so breit und doppelt so hoch sein wie die angegebene groesse.
Das heisst, du kannst bzw. musst mit groesse zweimal eine mathematische Operation (Division und Multiplikation) durchführen.
Wie du der nachfolgenden Tabelle entnehmen kannst, wird für die Multiplikation das *-Symbol verwendet und für die Division das /-Symbol.
| Operator | Beschreibung | Beispiel |
|---|---|---|
Addition, + | summiert zwei Zahlen | 5 + 2 = 7 |
Subtraktion, - | subtrahiert eine Zahl von einer anderen | 5 - 2 = 3 |
Multiplikation, * | bildet das Produkt zweier Zahlen | 5 * 2 = 10 |
Division, / | teilt eine Zahl durch eine andere | 5 / 2 = 2.5 |
Ganzzahldivision, // | teilt zwei Zahlen und rundet auf die nächstkleinere ganze Zahl ab | 5 // 2 = 2 |
Modulo, % | gibt den Rest einer Ganzzahldivision zurück | 5 % 2 = 1 |
Potenz, ** | potenziert eine Zahl mit einer anderen | 5 ** 2 = 25 |
Die Kleeblätter
Schreibe nun die zwei Funktionen kleeblatt_dreiblaettrig und kleeblatt_vierblaettrig. Überlege genau, wo welche (Teil)grafik ihre Fixierposition hat bzw. haben soll. Setze dann die Funktionen fixiere, kombiniere und drehe geschickt ein, um schliesslich die fertigen Kleeblätter mittels zeige_grafik anzeigen zu lassen.
Gut zu wissen
In dieser Aktivität verwenden wir vereinfachend die Bezeichnungenkleeblatt_dreiblaettrig und kleeblatt_vierblaettrig für die zu generierenden Funktionen. Diese Namen sind botanisch gesehen nicht ganz korrekt, da die verwendete teilblatt-Funktion herzförmige Teilblätter erzeugt, welche typisch für Sauerklee (Oxalis) sind, nicht für den botanischen Klee (Trifolium).
(Quelle: https://www.wikipedia.org)
Was du gelernt hast
Du hast verschiedene Kreissektoren gezeichnet und kannst nun auch die sehr potenten Funktionen für die Grafikkomposition mittels Fixierung (fixiere, kombiniere, Fixierpositionen wie oben_mitte) zu deinem Repertoir zählen.
Zudem hast du gelernt, wie in Python mathematische Operationen wie die Division (/) und die Multiplikation (*) zur Anwendung kommen können.
This activity has been created by Lichtsteiner and is licensed under CC BY-SA 4.0.
It is derived from this activity.
Grafikkomposition mittels Fixierung
PyTamaro is a project created by the Lugano Computing Education Research Lab at the Software Institute of USI
Privacy Policy • Platform Version 1cd5229 (Tue, 05 Nov 2024 16:55:57 GMT)