Fibonacci-Schnecke

In dieser Übung geht es darum, die for-Schleife noch besser kennen und nutzen zu lernen. Du wirst die ersten Zahlen der Fibonacci-Folge einsetzen, um das Gehäuse einer Schnecke zu implementieren.

Die Fibonacci-Folge ist die unendliche Folge natürlicher Zahlen, die mit zweimal der Zahl 1 beginnt, wobei jede Zahl die Summe ihrer beiden vorherigen Zahlen ist. In moderner Schreibweise wird dieser Folge oft eine führende 0 hinzugefügt:

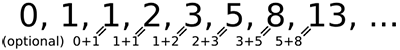
Die in dieser Folge enthaltenen Zahlen sind als Fibonacci-Zahlen bekannt. Sie erhielten ihren Namen von dem italienischen Mathematiker Leonardo Fibonacci, der im Jahr 1202 dieses Muster zur Beschreibung des Wachstums einer Kaninchenpopulation nutzte. Interessanterweise war die Fibonacci-Folge bereits in der Antike sowohl den Griechen als auch den Indern bekannt.

Weitere Untersuchungen haben gezeigt, dass die Fibonacci-Folge auch viele andere Wachstumsprozesse in der Natur beschreibt. Es scheint, als ob sie ein grundlegendes Muster für das Wachstum in der Natur darstellt.

Die Segmente

Das Schneckenhaus, oder allgemein die Fibonacci-Spirale, besteht aus farbigen Viertelkreisen, die gedreht und grösser werden.

Als Erstes müssen wir die segment Funktion erstellen. Diese gibt einen schwarzen Viertelkreis mit dem gewünschten Radius zurück, welcher so von einem kleineren Viertelkreis der angegebenen Farbe überdeckt wird, dass der Grossteil des schwarzen Sektors nicht mehr sichtbar ist. Damit wird die Illusion einer schwarzen Linie erzeugt. Die Differenz zwischen den Radien des schwarzen und des abdeckenden Viertelkreises entspricht dabei der angegebenen Linienstärke.

Um den gewünschten Effekt zu erzielen, musst du fixiere und kombiniere verwenden, um alles in der unteren linken Ecke zu fixieren.

Das Schneckenhaus

Richtig! Das Schneckenhaus entsteht, wenn man Viertelkreise mit Radien in den Grössen der Fibonacci-Zahlen zeichnet und sie neben- bzw. übereinander stellt.

Implementiere nun die Funktion schneckenhaus, die eine Spirale wie die oben zurückgibt. Nutze dazu eine for-Schleife und die ersten Fibonacci-Zahlen, wobei du die 0 und die erste 1 weglässt.

Tipp: Verwende in der for-Schleife drehe und entweder ueber oder neben.

Der Schneckenkörper

Für die Erstellung des Schneckenkörpers sind zwar eine ganze Menge Codezeilen, aber keine for-Schleifen nötig. Deshalb sind nachfolgend die Funktionen linkes_auge, rechtes_auge und schneckenkoerper schon implementiert.

Versuche nachzuvollziehen, was diese Codezeilen jeweils "tun" und führe sie dann aus!

Die Schnecke

Nun kannst du das Schneckenhaus und den Schneckenkörper in einer Grafik zusammenführen. Implementiere dazu die Funktion schnecke, die Argumente für die Parameter laenge, farbe_koerper und farbe_gehaeuse entgegennehmen können soll.

Was du gelernt hast

Du hast die for-Schleife für eine komplexe Grafikkomposition eingesetzt und dabei die ersten Zahlen der berühmten Fibonacci-Folge genutzt. Dabei hast du auch die Datenstruktur Liste verwendet und ein weiteres Mal gesehen, dass eine Liste, genau wie andere Datentypen, einer Variablen zugewiesen werden kann.

Ausserdem hast du geübt komplexe, verschachtelte Ausdrücke zu verstehen.