Imagine two people, it could be you and a friend, who want to exchange a secret. You want to agree on a secret that you both know, but no one else does.

Can you even do that if you can only talk in public and everything you say can be overheard?

Agreeing on a secret color in public

You could try to agree on a secret color, for example. The first part of this activity will guide you through a process to do that. In cryptography, such a process is known as a protocol for exchanging a key (a secret). More precisely, this is not a protocol for transporting a secret that one person chose in advance; instead, the two parties will end up agreeing on a secret.

Start by choosing a base color. As friends, you can pick an arbitrary number for the hue (say 60, which is a shade of yellow) and communicate it out loud.

Now, both you and your friend have to choose a private color. These two private colors will not be communicated to the other person, otherwise they wouldn't be private anymore. Remember? Anyone can hear.

We will use the name a to refer to your private color, and b to refer to your friend's private color. To emphasize further that these colors are private, we prefix them with two underscores. They are still valid names in Python!

Each person, independently, now mixes their color with the base color chosen at the beginning. Think of this as mixing paints in the real world. In our digital world, there are many possible strategies to mix colors: one way is to compute a weighted average.

These two mixed colors can be shared publicly. People can see them, but they cannot know the private color used in the mix.

For the last step, each person takes the other person's mixed color and mixes it again with their own private color. You will take your friend's mixed color (base_and_b) and mix it with your private color (__a). Your friend will do the same with your mixed color (base_and_a) and their private color (__b).

Is the secret color really secret?

Here is a visual recap of the process. Colors known to the public are shown in the middle, while the private colors for each person are shown on the left and right margins.

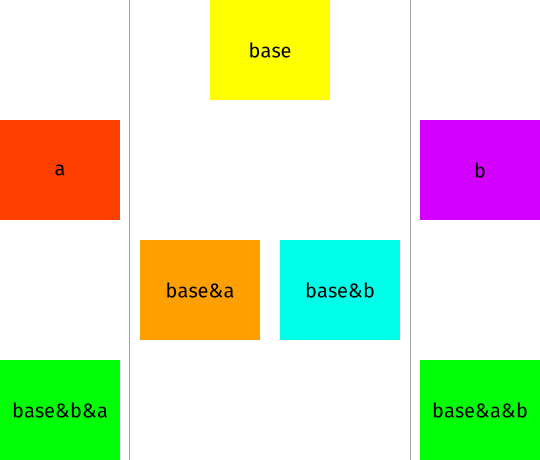
What makes this process supposedly secure is that unmixing colors is exceedingly hard. If one only knows the shade of orange base&a, they cannot unmix it to figure out the two colors used to create it.

But is the agreed secret color really secret?

Trying all possible private colors

The attacker could try all possible private colors, and see which one gives the same mixed color as the one they saw in public. If the number of colors is small enough, this is a feasible attack. In our case, if you only used integer numbers for the hue, there are only 360 possible private colors.

If you used integer numbers and implemented the attack correctly, you should have been able to find the private color you used. But even if you didn't, there is another strategy that an attacker could use.

Inverting mix

The attacker could also attempt to invert the mix function. Not only do they know how mix works and what the resulting mixed color is, but they also know one of the two colors used in the mix!

Equipped with this unmix function, the attacker can now immediately determine the private color used in the mix, and thus also compute the final color that was supposed to be a secret.

From Insecure to Secure Cryptographic Protocols

Our color exchange protocol resembles famous protocols actually used to exchange secrets (keys) in cryptography. Our implementation may appear reasonable, but is fundamentally insecure for the two reasons you just experienced.

First, if we can only choose among a small number of colors, the attacker can simply try all possible private colors. This brute-force attack is feasible in cryptographic protocols too if the number of possible private values, known as the keyspace, is small enough.

Second, the mixing function we used is easily invertible. It's not enough to assume that "color unmixing" is infeasible, because an attacker knows both the mixed color and one of the two colors used in the mix (the base color).

You may be left wondering: can one design a "mixing" function that is not easily invertible, even when one knows the result and one of the two arguments? A small number of mathematical functions satisfy this requirement, to the best of our knowledge. The Diffie-Hellman key exchange uses one such function, modular exponentiation, and follows the exact steps you implemented above. You can learn more about it on its Wikipedia page.