Binomial Products
Do you remember the following mathematical identity from middle school?
(a + b)2 = a2 + 2ab + b2
You can also write this as:
(a + b) (a + b) = a2 + 2ab + b2
Let's compose an animation that visually explains this equation!
Decompose the Animation
Watch the animation at the top right. Hover over it with your mouse to make it bigger.
Yeah, admit it, you saw it below! :) Anyways, the animation loops through five frames:
The first frame shows the product (a + b)(a + b) = (a + b)2. The next frames gradually add rectangles for the terms of the resulting polynomial: first a2, then ab, and another ab, and finally b2.
Decompose a Frame
Let's look at the final frame, which includes the most detail:
Yes, it consists of four colored rectangles (each with a black label overlaid on top of it), and two axes. The x-axis contains two labels (a and b), centered under the corresponding rectangles. The y-axis contains two labels (b and a, starting from top), centered left of the corresponding rectangles.
We could also see this graphic as a 3-by-3 table. The left column contains the y-axis, the bottom row contains the x-axis, and the bottom left cell is empty.
Implementation
Let's implement the animation.
What's All This About?
We visualized the following "notable product":
(a + b) (a + b) = a2 + 2ab + b2
On the left side of this equation we have a product of two bivariate (variables a and b) linear (degree 1) binomials (2 terms). On the right hand side we have the bivariate quadratic (degree 2) polynomial (composed of three terms) representing the result of the multiplication.
Polynomials?
A polynomial is an expression like 12x³ + 5x + (-3), built from:
- variables (like c or x or k, assuming c, x, or k are names that denote variables)
- constants (like the literal -3; or like c or x or k if these names denote constants)
- addition (like a + b)
- multiplication (like ab)
- exponentiation to a non-negative integer power (like a²)
Polynomials can be distinguished by the number of variables they contain:
- 0 - a constant polynomial does not contain any variable (like 42).
- 1 - a univariate polynomial contains exactly one variable (like 2x³).
- 2 - a bivariate polynomial contains exactly two variables (like 21x³y²).
- many - multivariate polynomial contains more than one variable (like 21x³y² or 21x³y²z).
Every univariate polynomial can be written in the form
anxn + an-1xn-1 + ... + a2x2 + a1x + a0
where an ... a0 are constants (also called coefficients of the polynomial) and x is the variable. We can more concisely represent the above expression using a sum:
Polynomials can be distinguished by the number of terms they are composed of:
- 0 - a zero polynomial is a polynomial consisting of zero terms. It has the value 0.
- 1 - a monomial is a polynomial consisting of one term, like 2a².
- 2 - a binomial is a polynomial consisting of two terms, like 3x³ + 5y².
- many - a polynomial consists of zero or more terms.
Polynomials also can be distinguished by their degree. The degree of a polynomial is the maximum of the degrees of its terms. The degree of a term is the sum of the exponents of the variables that appear in the term. Polynomials of degree:
- 0 - constant polynomial, like 42.
- 1 - linear polynomial, like 3x + 2y.
- 2 - quadratic polynomial, like 3x² + 2x + 10 or 3xy + 5.
- 3 - cubic polynomial, like 3x³ + 10 or 5xy² + 2x + 1.
Product of Polynomials?
The "notable product" we visualized is a product of two polynomials. Yes, you can multiply polynomials, like you can multiply two integer numbers.
Many operations you can do with numbers you can also do with polynomials! You can:
-
add two polynomials, and you get a polynomial as a result.
-
subtract two polynomials, and you get a polynomial as a result.
-
multiply two polynomials, and you get a polynomial as a result.
-
divide two polynomials, but the result is not necessarily a polynomial; the result of a division of two polynomials is a rational fraction.
You also can do other operations with polynomials, such as composing or factoring them.
Other Noteable Products
We visualized on "notable" product. There are others. Here is a short list of the "most notable" products of two bivariate (variables a and b) linear (degree 1) binomials (2 terms):
(a + b) (a + b) = a2 + 2ab + b2 -- usually just written as (a + b)2.
(a + b) (a - b) = a2 - b2
(a - b) (a - b) = a2 - 2ab + b2 -- usually just written as (a - b)2.
You may want to program visual explanations of the second and the third one. They are slightly trickier because of the subtractions, but they are totally doable. Give it a try!
Knowing these identities can help you, for example when you need to factorize a polynomial that looks like the ones on the right hand side of the above equations.
What You Learned
In terms of composing graphics by composing programs, you practiced composing a tabular structure and composing an animation from frames.
You also reviewed the fundamental math concept of a polynomial that you may have first met in middle school, and that is usually covered in more depth in high school.
This activity has been created by LuCE Research Lab and is licensed under CC BY-SA 4.0.
Binomial Products
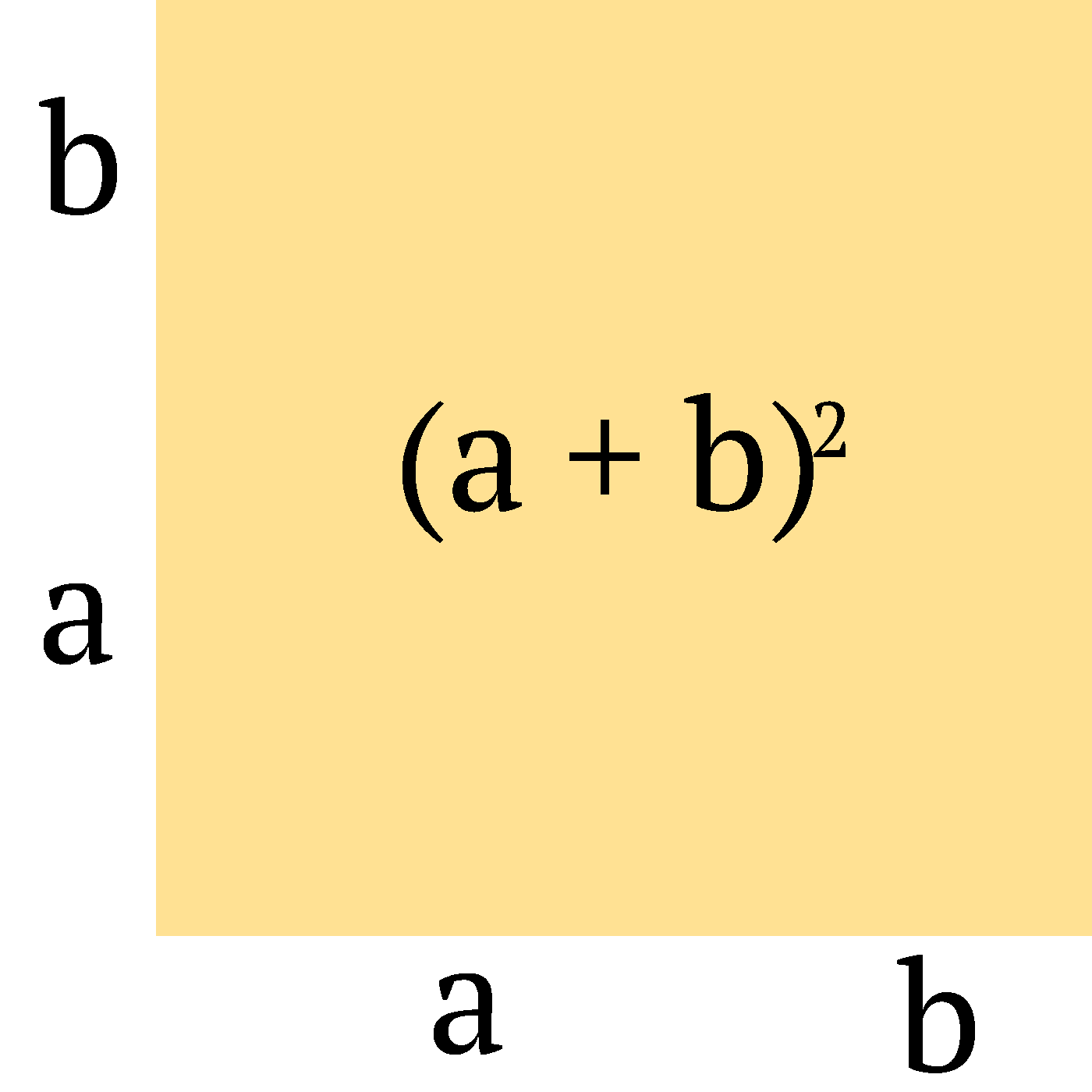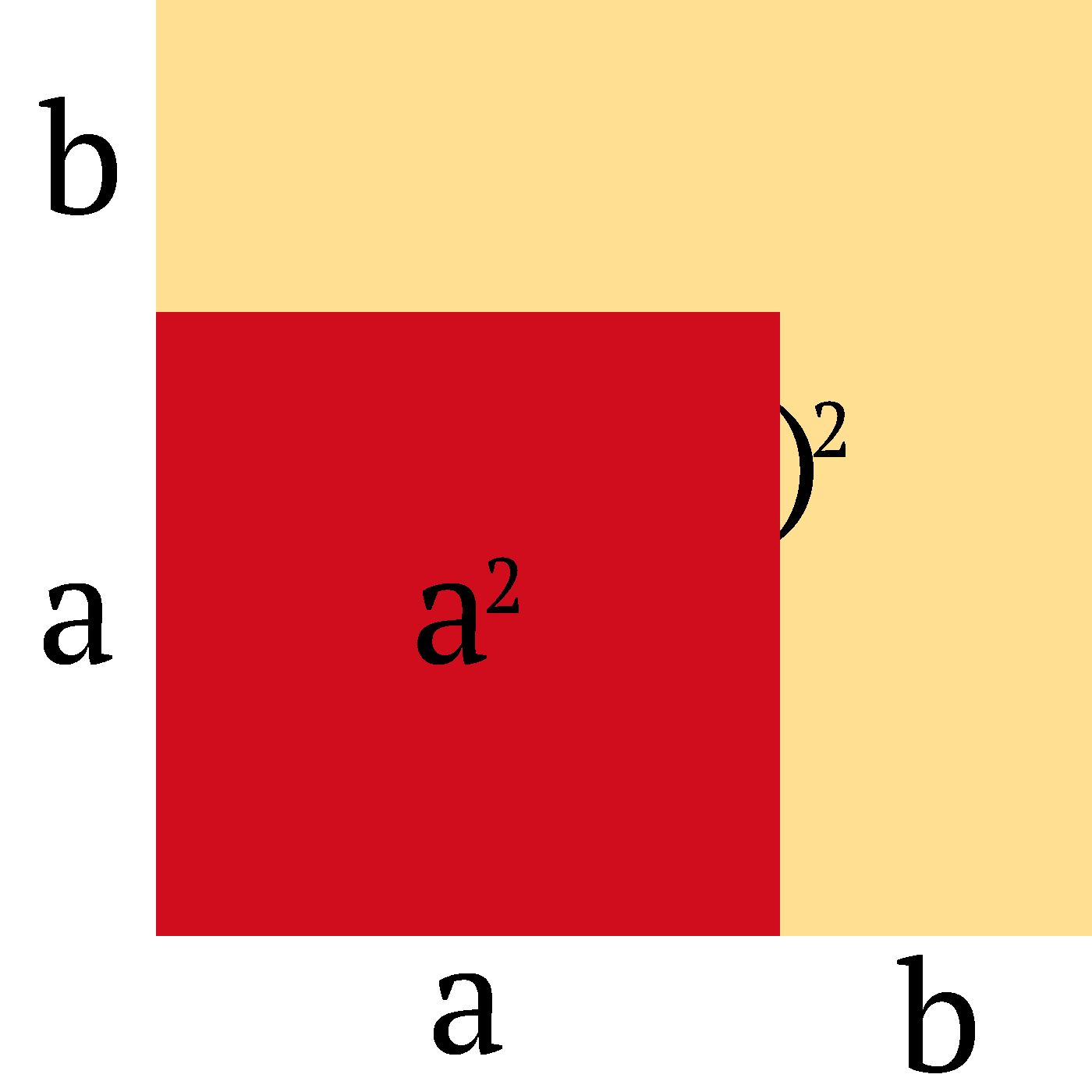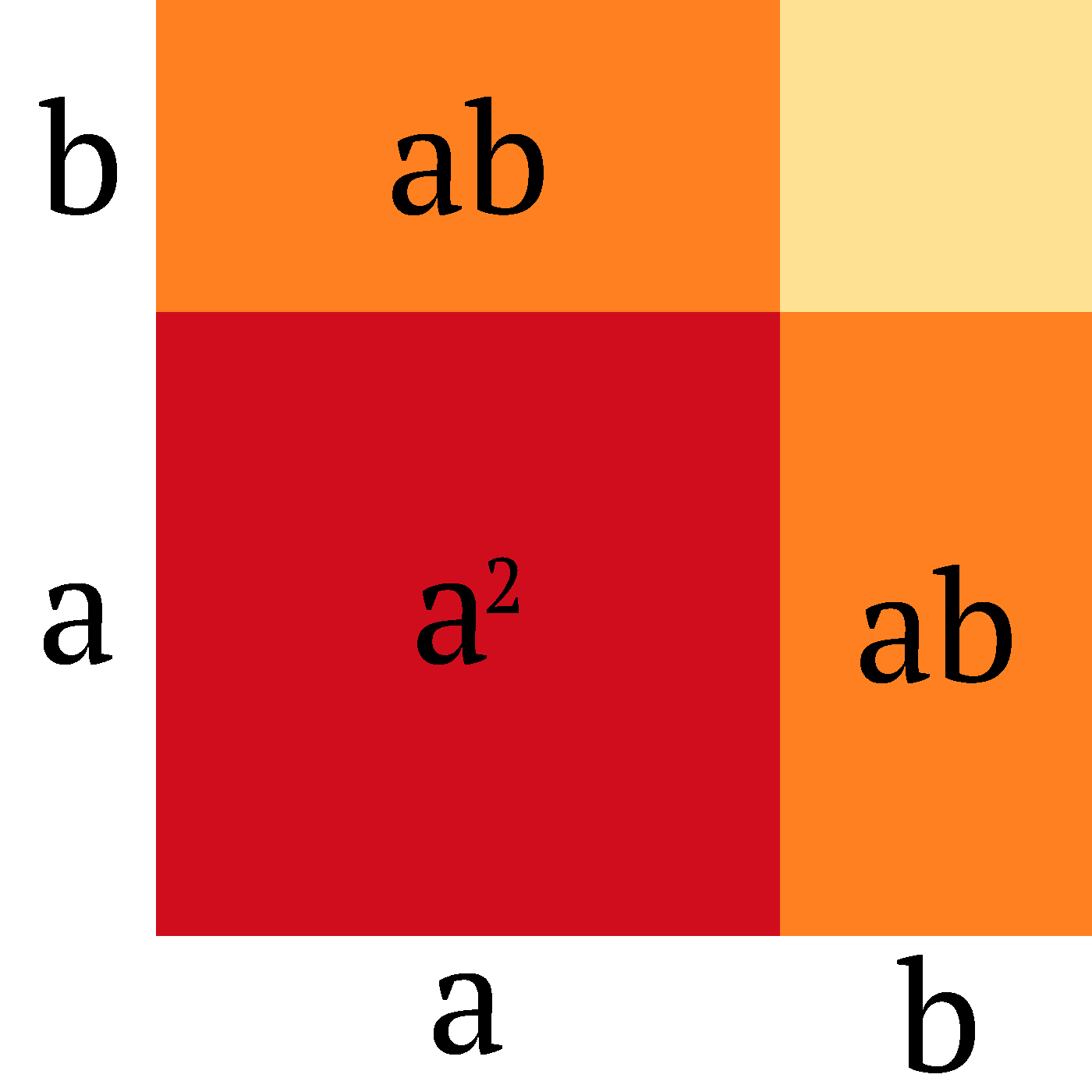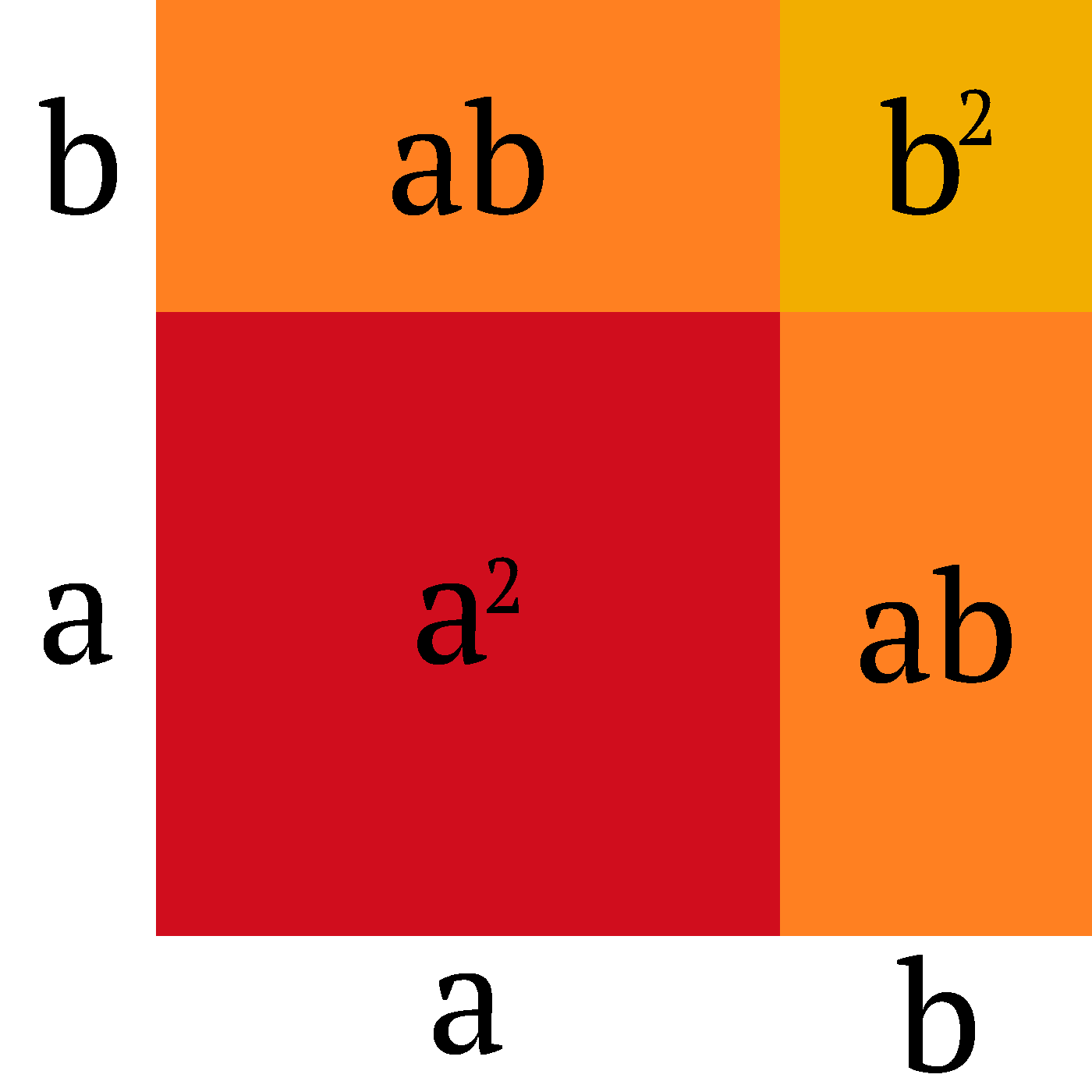

PyTamaro is a project created by the Lugano Computing Education Research Lab at the Software Institute of USI
Privacy Policy • Platform Version f5b96bc (Sun, 04 Jan 2026 17:27:49 GMT)
