Balkendiagramm

In dieser Aktivität wirst du einen Typ Grafik erstellen, den du wohl eher mit einem Programm wie z.B. Microsoft Excel oder Apple Numbers in Verbindung bringst: das Balkendiagramm.

Mit der Fibonacci-Folge zum Drohnenstammbaum

(Quelle: Wikipedia-Artikel "Fibonacci-Folge)

In der optionalen Aktivität Fibonacci-Schnecke hast du gelernt, dass die Fibonacci-Folge ihren Namen von Leonardo Fibonacci hat. Er beschrieb in seinem Liber abbaci („Buch der Rechenkunst“, Erstfassung von 1202 nicht erhalten, zweite Fassung von ca. 1227) diese Zahlenfolge mit dem Beispiel eines Kaninchenzüchters, der herausfinden will, wie viele Kaninchenpaare innerhalb eines Jahres aus einem einzigen Paar entstehen, wenn jedes Paar ab dem zweiten Lebensmonat ein weiteres Paar pro Monat zur Welt bringt. Dabei galten folgende (vereinfachende) Regeln:

1. Jedes Paar Kaninchen zeugt jeden Monat ein zusätzliches Paar Kaninchen.

2. Ein neugeborenes Paar bringt erst im zweiten Lebensmonat seines Lebens Nachkommen zur Welt (die Tragzeit erstreckt sich über einen Monat in den nächsten).

3. Die Kaninchen befinden sich in einem abgeschlossenen Raum („in quodam loco, qui erat undique pariete circumdatus“), wodurch keine Tiere die Population verlassen können, und kein Zugang von aussen möglich ist.

Fibonacci startete die Abfolge, wenn auch nicht völlig konsequent, nicht mit einem neugeborenen Paar, sondern mit einem trächtigen Paar, das bereits im ersten Monat Nachwuchs zeugte. Daher gibt es bereits im ersten Monat 2 Paare zu zählen. In jedem darauf folgenden Monat wird zu der Anzahl der Paare, die im vorherigen Monat überlebt haben, eine Anzahl von neugeborenen Paaren hinzugefügt. Diese Anzahl entspricht der Anzahl der Paare, die bereits im vorvergangenen Monat existierten, da der Nachwuchs des vorherigen Monats noch zu jung ist, um in diesem Monat selbst Nachwuchs zu zeugen. Fibonacci präsentierte dieses Konzept für die zwölf Monate eines Jahres (2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377) und betonte, dass die Folge durch die Addition von jeweils zwei aufeinanderfolgenden Elementen (2 + 3 = 5, 3 + 5 = 8, 5 + 8 = 13 usw.) gebildet wird. Er wies auch darauf hin, dass diese Abfolge nach diesem Prinzip für eine unendliche Anzahl von Monaten fortgesetzt werden kann. Dies würde jedoch unsterbliche Kaninchen voraussetzen: „et sic posses facere per ordinem de infinitis numeris mensibus.“

Die folgende Darstellung illustriert das Wachstum einer Kaninchenpopulation, beginnend mit einem neugeborenen Paar. Die roten und blauen Eier symbolisieren die Zeugungsfähigkeit des betreffenden Kaninchens. Kaninchen, die kein Ei halten, können entsprechend noch keine Nachkommen zeugen.

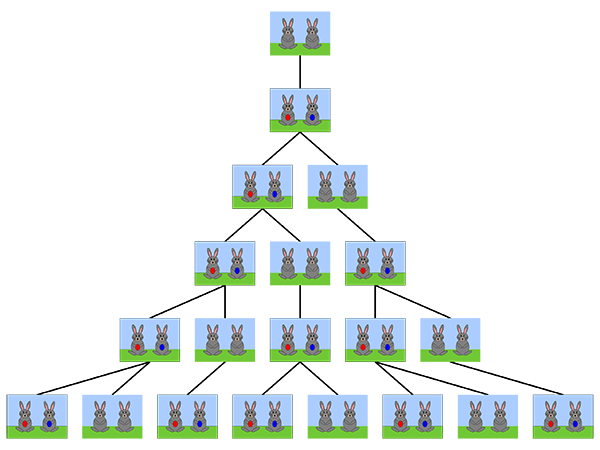
Allerdings kam eine 2014 erschienene, mathematisch-historische Analyse zum Leben von Leonardo Fibonacci, insbesondere zu seinem Aufenthalt in der nordafrikanischen Hafenstadt Bejaia (im heutigen Algerien), zu dem Schluss, dass der Hintergrund der Fibonacci-Folge gar nicht bei einem Modell der Vermehrung von Kaninchen zu suchen ist, sondern vielmehr bei den Bienenzüchtern von Bejaia und ihrer Kenntnis des Bienenstammbaums zu finden ist.

Männliche Bienen, auch als Drohnen bezeichnet, haben eine interessante Verbindung zur Fibonacci-Folge. Dies kommt daher, dass die Anzahl der Vorfahren einer Drohne durch diese Folge beschrieben wird. Dies kann erklärt werden, da eine Drohne (Generation n = 1) aus einem unbefruchteten Ei stammt, das nur das Erbgut ihrer Mutter, der Bienenkönigin (Generation n = 2), enthält. Eine Drohne hat keinen Vater. Im Gegensatz dazu hat eine Bienenkönigin zwei Eltern: eine andere Königin als Mutter und eine Drohne als Vater (Generation n = 3) usw. Die Anzahl der Vorfahren einer Drohne in je einer so definierten n-ten Generation entspricht der n-ten Fibonacci-Zahl.

Um das einzusehen, lässt sich die obige Darstellung zur Anzahl der Kaninchen in Fibonaccis Modell verwenden. Jedes Paar nicht geschlechtsreifer Kaninchen entspricht einer Drohne, jedes Paar geschlechtsreifer Kaninchen einer Königin.

Baue nun Schritt für Schritt die Elemente, mit welchen du schliesslich das Balkendiagramm von oben erstellen kannst.

Die Funktion baustein

Implementiere als Erstes die Funktion baustein, die sowohl einen roten D(rohne)-Baustein als auch einen grünen K(önigin)-Baustein erstellen kann. Nutze dazu die Funktion text und die Schriftart Fira Code.

Die Funktion fibonacci_zahlen

Schreibe eine fibonacci_zahlen Funktion, die die ersten n + 1 Fibonacci-Zahlen (inkl. 0) als Liste zurückgibt. Wenn du Hilfe benötigst, hilft ein Blick in die Aktivität Fibonacci-Schnecke.

Die Funktion vorfahren_balken

Nutze deine fibonacci Funktion, um eine vorfahren_balken Funktion zu erstellen. Diese Funktion soll einzelne Balken für das schlussendlich gewünschte Balkendiagramm erstellen können.

Ein Balken besteht aus nebeneinandergereihten K- und D-Bausteinen. Dabei gilt:

• Die totale Anzahl Bausteine entspricht der Anzahl Vorfahren einer Drohne (n = 1) in einer n-ten Generation. Diese Anzahl entspricht der n-ten Fibonacci-Zahl.
• Die Anzahl K-Bausteine entspricht der n-1-ten Fibonacci-Zahl.
• Die Anzahl D-Bausteine entspricht der n-2-ten Fibonacci-Zahl.

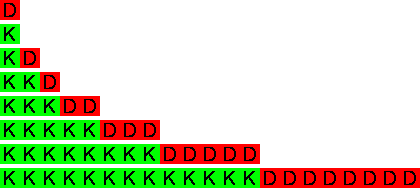
So soll der Aufruf vorfahren_balken(6, 20) die nachfolgende Balken-Grafik erzeugen, da 8 die sechste Fibonacci-Zahl ist (exkl. 0) und sich aus den Fibonacci-Zahlen 5 und 3 zusammensetzt.

Die Funktion vorfahren_balkendiagramm

Schreibe zum Schluss eine vorfahren_balkendiagramm Funktion, die eine Drohne mit all ihren Vorfahren als Balkendiagramm darstellt.

Beispielsweise soll der Aufruf vorfahren_balkendiagramm(8, 20) folgende Grafik zurückgeben.